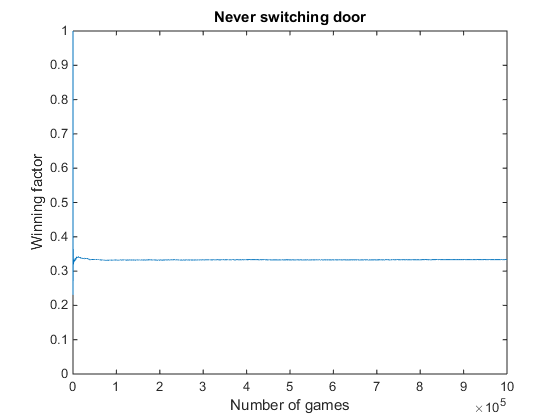
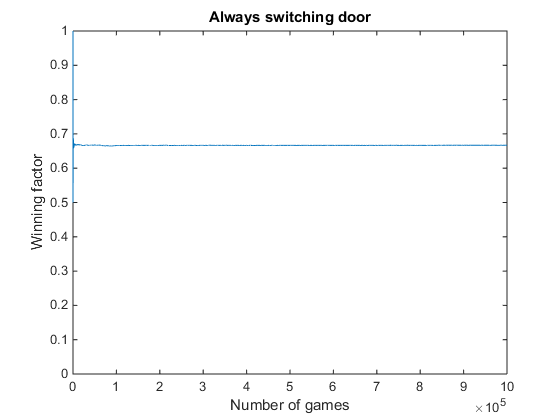
Empirical proof of the Monty Hall statistics

for k = 1:2

Switch = k-1; % Switch = 1, not switch = 0
games = 1000000;
correct = 0;

    for i = 1:games

    doors = [1 2 3];
    car = doors(randi(numel(doors))); % Random placing of car
    choice = doors(randi(numel(doors))); % Random choice of door

        % Random opening a door with goat
        if choice == car
            doors(doors==car) = [];
            open = doors(randi(numel(doors)));
        else
            doors(doors==car) = [];
            doors(doors==choice) = [];
            open = doors;
        end
    %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

        if Switch == 1
        schoice = [1 2 3];
        schoice(schoice==choice) = [];
        schoice(schoice==open) = [];
        else
        schoice = choice;
        end

        if schoice == car
           correct = correct + 1;
        end
        res(i) = correct/i;

        end
        figure
        plot(res)
        if Switch == 1
            title('Always switching door')
        else
            title('Never switching door')
        end

        axis([0 games 0 1])
        xlabel('Number of games')
        ylabel('Winning factor')

        if Switch == 1
        Result_switch = correct/games
        else
        Result_noswitch = correct/games
        end

end

Result_noswitch =

    0.3335


Result_switch =

    0.6669